잡학사전/기타(etc.)
3x3 큐브 공식, 100% 성공 방법!
노하우저장소
2022. 5. 22. 19:28
큐브 풀이 설명서 인쇄용 다운로드
3x3 큐브 공식 - 노하우저장소.pdf
0.29MB
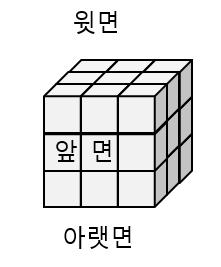
큐브 면 정의
기준면은 편의상 흰색으로 정하였습니다. 그리고 기준면 반대쪽은 본 예시의 경우 노랑이 됩니다.
그리고 큐브를 바라볼 때 각 면은 오른쪽 그림과 같이 정의하였습니다.
공식은 항상 윗면을 보는 상태에서 적용합니다.
블록의 이동을 표현하는 화살표
- 초기 위치는 화살표의 시작 점으로 표시했습니다.
- 이동 후 위치는 화살촉 끝이 속한 면에 해당합니다.
- 화살촉이 면에 들어가지 못한 경우, 그림상 눈에 보이지 않는 측면, 뒷면 또는 아랫면으로 이동했다는 의미입니다.
- 점선 화살표는 블록 제거 시 참고할 이동 경로입니다.
- 검은색 점만 표시된 경우, 해당 블록은 위치가 변경되지 않는다는 의미입니다.
공식 약호 뜻
| 약호 | 뜻 | 약호 | 뜻 | 약호 | 뜻 | 약호 | 뜻 |
| 내 | 내림 | 시 | 시계 방향 돌림 | 오 | 오른쪽 | 돌 | 동일 방향으로 돌림 |
| 올 | 올림 | 반 | 반시계 방향 돌림 | 왼 | 왼쪽 | - | - |
단계별 공식 및 설명
기준면(흰색) 十자 만들기
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
없음 | - | - |
| 별도 공식이 없으며 비교적 간단히 방법을 찾을 수 있음. | |||
十자 옆면 일치시키기
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
 |
 |
- |
| 十(십)자 만든 후 최소 2개의 옆면은 항상 일치. 위치가 바뀌지 않는 두 곳의 블록을 고정시키고 공식 적용. Case #1 - 공식의 효과 그림과 같이 이웃한 면과 서로 바꿀 경우 공식 1회 적용으로 완성. Case #2 - 공식의 효과 그림과 달리 바꿀 블록이 반대편에 있는 경우 공식 1회 적용하여 Case #1과 같이 만든 후 공식 1회 추가 적용 (총 2회) |
|||
(기준면을 아래로 향하게 뒤집은 뒤)
아래쪽 T자 만들기
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
 |
 |
 |
| 윗면(T자로 만들 색상)이 앞면으로, 앞면이 옆면으로 이동되므로 두 색상이 모두 일치하도록 블록을 위치시킨 뒤 공식 적용. ※ 이동할 블록이 없는 경우 (노랑 十자 상태일 경우) 아무 위치에서 공식을 적용하면 이동 가능한 블록이 1개 생김. |
|||
기준면(흰색) 쪽 2단 맞추기
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
 |
 |
 |
| 앞면(흰색)이 아랫면(기준면)으로 이동되도록 공식 반복 적용. ※ 흰색면을 가진 블록이 기준면 꼭지에 위치했지만 측면 색상이 불일치하는 경우 공식을 적용해 윗면으로 이동 (점선 참고) ※ 예시와 같이 다른 두 면의 색상도 일치한 상태에서 공식 적용할 것. |
|||
기준면 반대쪽(노랑색) 十자 만들기
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
 |
 |
 |
| 1) 먼저 一(일)자를 만들어야 하며, 노랑색이 예시와 같은 상태에서 공식을 적용. ※ 해당 형태가 없을 시 공식 1회 적용. 2) 一자 상태에서 공식 1회 적용하면 十자 완성. |
|||
기준면 반대쪽(노란색)十자 옆면 일치시키기
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
 |
 |
- |
| 十자 만든 후 최소 2개 위치는 항상 일치. Case #1 - 공식의 효과 그림과 같이 옆면과 서로 바꿀 경우 공식 1회 적용으로 완성. Case #2 - 공식의 효과 그림과 달리 바꿀 블록이 반대편에 있는 경우 공식 1회 적용하여 Case #1과 같이 만든 후 공식 1회 추가 적용 (총 2회) |
|||
기준면 반대쪽 색상(노랑색) 일치시키기
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
 |
 |
 |
| Case #1 - 꼭지가 맞춰진 것이 하나도 없는 경우 공식 1회 적용. Case #2 – 탱크형. 예시 방향에서 공식 1회 적용하여 나비 넥타이형 또는 물고기형 완성. Case #3 – 물고기형. 예시 방향에서 공식 1회 적용하여 나비 넥타이형 또는 탱크형 완성. Case #4 - 나비 넥타이형. 초록색 화살표면에 노랑색(기준면 반대 색상)이 위치되도록 잡고 공식 적용하여 완성. |
|||
마무리 (꼭지 옆면 맞추기)
| 최종 목표 | 활용 공식 (외울 때) | 공식의 효과 | 예시 |
 |
 |
 |
- |
| 삼면이 일치하는 꼭지를 고정되는 위치에 놓고 공식 반복 적용함. (최대 2회) ※ 일치하는 꼭지가 없는 경우, 공식 1회 적용해 일치하는 꼭지가 1개 생기도록 함. |
|||
이상입니다.